
|
The source is here.
- Points of interest
- use of iterative equation solver
- convolution with the Green's function
- use of diffuse domain approximation to represent interior surfaces
- line and volume plots
- imposition of exterior Neumann boundary conditions
- Background
We wish to solve Laplaces's equation within a non-homogeneous medium, i.e., in which the permittivity is not constant, with an external electric field.
![\[ \nabla . \left( \epsilon(r) \nabla v(r) \right) = 0 \]](form_118.png)
Expanding and rearranging yields,
![\[ \nabla^2 v(r) = - \frac{1}{\epsilon} \nabla \epsilon(r) . \nabla v(r) \]](form_119.png)
We can interpret 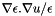 as the induced surface charge density.
as the induced surface charge density.
MADNESS's default Coulomb Green's function ( 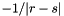 ) corresponds to the free-space Dirichlet boundary condition
) corresponds to the free-space Dirichlet boundary condition 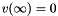 . But we wish to impose the Neumann condition
. But we wish to impose the Neumann condition 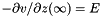 . Thus, we write our solution as the sum of the asymptotic solution (
. Thus, we write our solution as the sum of the asymptotic solution ( 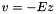 ) and a component that goes to zero at infinity so that our MADNESS Green's function can be used. Substituting
) and a component that goes to zero at infinity so that our MADNESS Green's function can be used. Substituting
![\[ v(r) = - E z + u(r) \]](form_124.png)
our equation becomes
![\[ \nabla^2 u(r) = \frac{1}{\epsilon} \nabla \epsilon(r) . \left(E - \nabla u(r) \right) \]](form_125.png)
The quantity in parentheses is the total electric field — the sum of the applied field and that due to the induced surface charge.
The exact solution is readily derived by expanding in spherical harmonics and matching the potential and electric displacement at the surface, or by looking inside Jackson, or by a quick google to find this page.
(Note that while the Green's function to Poisson's equation is 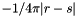 , MADNESS provides convolution with
, MADNESS provides convolution with 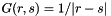 , so you have to keep track of the
, so you have to keep track of the 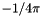 yourself.)
yourself.)
(Note that to obtain an accurate solution with 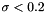 you will need to increase the order of the wavelet and decrease the threshold, e.g.,
you will need to increase the order of the wavelet and decrease the threshold, e.g., 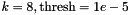 .
.
 1.8.8
1.8.8