
|
The source is here.
- Points of interest
- application of the Coulomb and Helmholtz Green's functions
- smoothing of the potential and initial guess
- manual evaluation of the solution along a line
- Background
The Hartree-Fock wave function is computed for the helium atom in three dimensions without using spherical symmetry.
The atomic orbital is an eigenfunction of the Fock operator
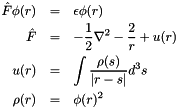
that depends upon the orbital via the Coulomb potential ( 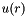 ) arising from the electronic density (
) arising from the electronic density ( 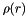 ).
).
- Implementation
Per the usual MADNESS practice, the equation is rearranged into integral form
![\[ \phi = - 2 G_{\mu} * ( V \phi) \]](form_144.png)
where 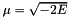 and
and 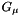 is the Green's function for the Helmholtz equation
is the Green's function for the Helmholtz equation
![\[ \left( - \nabla^2 + \mu^2 \right) G(r,r^{\prime}) = \delta(r,r^{\prime}) \]](form_147.png)
The initial guess is  , which is normalized before use. Each iteration proceeds by
, which is normalized before use. Each iteration proceeds by
- computing the density by squaring the orbital,
- computing the Coulomb potential by applying the Coulomb Green's function,
- multiplying the orbital by the total potential,
- updating the orbital by applying the Helmholtz Green's function,
- updating the energy according to a second-order accurate estimate (see the initial MRQC paper), and finally
- normalizing the new wave function.
The kinetic energy operator is denoted by 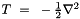 . Thus, one would expect to compute the kinetic energy with respect to a wave function
. Thus, one would expect to compute the kinetic energy with respect to a wave function  by
by 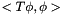 . In this particular example, the wave functions goes to zero smoothly before the boundary so we apply the product rule for differentiation and the kinetic energy is equal to
. In this particular example, the wave functions goes to zero smoothly before the boundary so we apply the product rule for differentiation and the kinetic energy is equal to 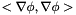 .
.
The source is here.
 1.8.8
1.8.8