Collaboration diagram for Solves a Navier-Stokes equation:

The source is here.

Points of interest

convolution with periodic Green's function (Possion/Coulomb kernel and Modified Helmholtz/Bound State Helmholtz/Yukawa kernel)
output data for ParaView

Background: This illustrates the solution of a Navier-Stokes equation for incompressible flows,
$\begin{eqnarray*} u_t - u \cdot \nabla u + \nabla p & = &\mu \Delta u + f \\ \nabla \cdot u & = & 0 \end{eqnarray*}$
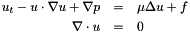
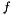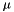where the force and the viscocity and $\mu$ are given in the code.

Implementation

Step 1. Calculate the pressure at time 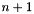$ n+1 $ explicitly.

$\Delta p = \nabla \cdot (f - u_{n} \cdot \nabla u_{n} )$

Everything in the RHS is either given or known; thus 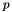$p$ can be obtained by applying a Coulomb operator.

Step 2. Calculate the velocity at time n+1.

$(\frac{1}{ \delta t \mu } - \Delta) u_{n+1} = \frac {f - \nabla p - u_n \cdot \nabla u_n }{ \mu } + \frac {u_n}{ \delta t \mu }$

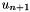Again, $u_{n+1}$ is calculated by applying the BSH operator to the RHS.

The resulting method is a first order in time scheme and can be extended by Spectral/Krylov deferred corrections to construct higher order methods. Particularly, the construction of a second order scheme under this frame is easy and similar to the Crank-Nicolson technique, which is also demonstrated by the example.

Reference: Jia, J.; Hill, J.; Fann, G. & Harrison, R. J. MULTIRESOLUTION FAST METHODS FOR A PERIODIC 3-D NAVIER-STOKES SOLVER Proceedings of the Eighth International Symposium on Distributed Computing and Applications to Business, Engineering and Science, Publishing House of Electronics Industry, 2009