Collaboration diagram for Solves a 1D time-dependent Schrödinger equation using splitting and semi-group approaches with the free-particle propagator.:

The source is here.

Points of interest

convolution with the Green's function/free-particle propagator
use free-particle propagators construct different schemes to find the solution
collocation methods on quadrature points

Background: This illustrates solution of a time-dependent Schrödinger equation.

We solve the following PDE

$-\nabla^2 \psi(x,t) + V(x,t) \psi(x,t) = i\psi_t(x,t)$

where the potential is

$V(x,t) = -8 \exp((x - v \cdot t)^2)$

and the velocity 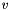$ v $ is given in the code.

Implementation

Splitting based schemes, such as Trotter and Chin-Chen, can be found in existing literatures.

The quadrature collocation method is based on the semi-group form of the equation

$\psi(x,t) = \psi(x,0) * G(x,t) - \int_0^t V(x,s) \cdot \psi(x,s) * G(x,t-s) ds$

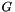where $ G $ is the Green's function/free-particle propagator

$\left( - \frac{d^2}{dx^2} - i \frac{d}{dt} \right) G(x) = \delta(x)).$

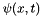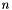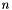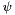To find $\psi(x,t)$ , all temporal integrals are computed by a $n$ point Gauss-Legendre quadrature rule and we need to calculate employ a simple fixed-point iteration to the self-consistent solutions at the $n$ quadrature points on the intervel $ [0,t] $ . All $\psi$ involved in computing the integrals over the subintervels are interpolated by the 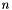$n$ values on the largest intervel .

The fixed-point iteration is applied to the correction term of the semi-group formulation,

$\psi^{m+1}(x,t) - \psi^{m}(x,t) = - \int_0^t V(x,s) \cdot ( \psi^{m}(x,s) - \psi^{m-1}(x,s)) * G(x,t-s) ds$

or

$\delta^{m+1}(x,t) = - \int_0^t V(x,s) \cdot \delta^{m}(x,s) * G(x,t-s) ds$

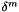where $\delta^m$ is the $m_{th}$ correction term.

A much more efficient scheme would involve use of a non-linear equation solver instead of simple iteration.

Once we have the solutions at the 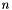$n$ quadrature points on $ [0,t] $ , quadrature rule is used to construct the solution at 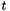$t$ .

Reference: Preprint.