
|
The source is here.
This example computes the energy of the ground state of the hydrogen atom as the expectation value of the non-relativistic Schrödinger Hamiltonian within the Born-Oppenheimer approximation. Explicitly,
![\[ E = \frac{\langle \psi \mid - \frac{1}{2} \nabla^2 - \frac{1}{r} \mid \psi \rangle}{\langle \psi \mid \psi \rangle} \]](form_128.png)
where the unnormalized wave function is
![\[ \psi(r) = e^{-r} \]](form_129.png)
- Implementation
Two functions are required - the wave function and the potential. Note the small constants introduced to eliminate the cusp in the wave function and the singularity in the potential. Due to the volume element this smoothing has negligible effect on the result (perturbation theory can make this rigorous).
The wave function is exponentially decaying and has the value 2e-9 at r=20, so we pick this as a box size that is effectively infinite.
Using integration by parts and noting that 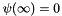
![\[ \langle \psi \mid \nabla^2 \mid \psi \rangle = - \langle \nabla \psi \mid \nabla \psi \rangle \]](form_131.png)
Finally, due to the spherical symmetry we only need compute one component of the Laplacian in Cartesian coordinates.
The exact answer is 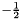 in atomic units.
in atomic units.
 1.8.8
1.8.8