
|
The source is here.
- Points of interest
- high-order integration of general time-dependent problems
- semigroup approach
- Background
Given 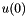 , we seek to solve the PDE
, we seek to solve the PDE
![\[ \frac{du}{dt} = \hat{L} u + N(u) \]](form_186.png)
for the function at some future time 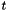 (i.e., for
(i.e., for 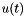 ).
). 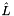 is a linear operator that we are able to exponentiate, and
is a linear operator that we are able to exponentiate, and 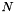 is everything else including linear and non-linear parts.
is everything else including linear and non-linear parts.
In the semigroup approach the formal solution to the PDE is written
![\[ u(t) = \exp(t \hat{L} ) u(0) + \int_0^t \exp((t-\tau)\hat{L}) N(u(\tau)) d\tau \]](form_191.png)
Numerical quadrature of the integral using Gauss-Legendre quadrature points is used resulting in a set of equations that are iteratively solved (presently using simple fixed point iteration from a first-order explicit rule).
The user provides
- functors to apply the exponential and non-linear parts, and
- if necessary a user-defined data type that supports a copy constructor, assignment, inplace addition, multiplication from the right by a double, and computation of the distance between two solutions
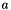 and
and 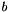 with the api +double distance(a,b)+
with the api +double distance(a,b)+
Have a look in testspectralprop.cc for example use.
With 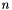 quadrature points, the error is
quadrature points, the error is 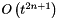 and the number of applications of the exponential operator per time step is
and the number of applications of the exponential operator per time step is 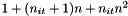 where
where 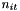 is the number of iterations necessary to solve the equations (typically about 5 but this is problem dependent).
is the number of iterations necessary to solve the equations (typically about 5 but this is problem dependent).
 1.8.8
1.8.8