Simplified interface to XC functionals. More...

#include <xcfunctional.h>

Public Member Functions
	XCfunctional ()
	Default constructor is required. More...

void	initialize (const std::string &input_line, bool polarized)
	Initialize the object from the user input data. More...

	~XCfunctional ()
	Destructor. More...

bool	is_lda () const
	Returns true if the potential is lda. More...

bool	is_gga () const
	Returns true if the potential is gga (needs first derivatives) More...

bool	is_meta () const
	Returns true if the potential is meta gga (needs second derivatives ... not yet supported) More...

bool	is_dft () const
	Returns true if there is a DFT functional (false probably means Hatree-Fock exchange only) More...

bool	is_spin_polarized () const
	Returns true if the functional is spin_polarized. More...

bool	has_fxc () const
	Returns true if the second derivative of the functional is available (not yet supported) More...

bool	has_kxc () const
	Returns true if the third derivative of the functional is available (not yet supported) More...

double	hf_exchange_coefficient () const
	Returns the value of the hf exact exchange coefficient. More...

madness::Tensor< double >	exc (const std::vector< madness::Tensor< double > > &t, const int ispin) const
	Computes the energy functional at given points. More...

madness::Tensor< double >	vxc (const std::vector< madness::Tensor< double > > &t, const int ispin, const int what) const
	Computes components of the potential (derivative of the energy functional) at np points. More...

void	plot () const
	Crude function to plot the energy and potential functionals. More...

Static Protected Member Functions
static void	polyn (const double x, double &p, double &dpdx)
	Smoothly switches between constant (x<xmin) and linear function (x>xmax) More...

static double	munge (double rho)

static void	munge2 (double &rho, double &sigma)

static void	munge_der (double &rhoa, double &sigma, double &drx, double &dry, double &drz)

static void	munge5 (double &rhoa, double &rhob, double &saa, double &sab, double &sbb)

static void	munge5_der (double &rhoa, double &rhob, double &saa, double &sab, double &sbb, double &drax, double &dray, double &draz, double &drbx, double &drby, double &drbz)

Protected Attributes
bool	spin_polarized
	True if the functional is spin polarized. More...

double	hf_coeff
	Factor multiplying HF exchange (+1.0 gives HF) More...

Detailed Description

Simplified interface to XC functionals.

Constructor & Destructor Documentation

XCfunctional::XCfunctional ( )

Default constructor is required.

XCfunctional::~XCfunctional ( )

Destructor.

Member Function Documentation

madness::Tensor< double > XCfunctional::exc	(	const std::vector< madness::Tensor< double > > &	t,
		const int	ispin
	)		const

Computes the energy functional at given points.

This uses the convention that the total energy is $E[\rho] = \int \epsilon[\rho(x)] dx$

Any HF exchange contribution must be separately computed.

Items in the vector argument t are interpreted as follows

Spin un-polarized
- t[0] =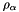 $\rho_{\alpha}$
- t[1] =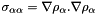 $\sigma_{\alpha\alpha} = \nabla \rho_{\alpha}.\nabla \rho_{\alpha}$ (GGA only)
Spin polarized
- t[0] =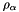 $\rho_{\alpha}$
- t[1] =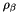 $\rho_{\beta}$
- t[2] =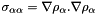 $\sigma_{\alpha\alpha} = \nabla \rho_{\alpha}.\nabla \rho_{\alpha}$ (GGA only)
- t[3] =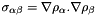 $\sigma_{\alpha\beta} = \nabla \rho_{\alpha}.\nabla \rho_{\beta}$ (GGA only)
- t[4] =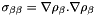 $\sigma_{\beta\beta} = \nabla \rho_{\beta}.\nabla \rho_{\beta}$ (GGA only)

Parameters

t	The input densities and derivatives as required by the functional

Returns: The exchange-correlation energy functional

change

References c_rks_vwn5__(), c_uks_vwn5__(), madness::f, L, munge(), spin_polarized, x_rks_s__(), and x_uks_s__().

Referenced by xc_functional::operator()(), and plot().

bool XCfunctional::has_fxc ( ) const

Returns true if the second derivative of the functional is available (not yet supported)

bool XCfunctional::has_kxc ( ) const

Returns true if the third derivative of the functional is available (not yet supported)

double XCfunctional::hf_exchange_coefficient ( ) const

inline

Returns the value of the hf exact exchange coefficient.

References hf_coeff.

void XCfunctional::initialize	(	const std::string &	input_line,
		bool	polarized
	)

Initialize the object from the user input data.

Parameters

[in]	input_line	User input line (without beginning XC keyword)
[in]	polarized	Boolean flag indicating if the calculation is spin-polarized

References hf_coeff, and spin_polarized.

bool XCfunctional::is_dft ( ) const

Returns true if there is a DFT functional (false probably means Hatree-Fock exchange only)

References is_gga(), is_lda(), and is_meta().

bool XCfunctional::is_gga ( ) const

Returns true if the potential is gga (needs first derivatives)

Referenced by is_dft().

bool XCfunctional::is_lda ( ) const

Returns true if the potential is lda.

References hf_coeff.

Referenced by is_dft().

bool XCfunctional::is_meta ( ) const

Returns true if the potential is meta gga (needs second derivatives ... not yet supported)

Referenced by is_dft().

bool XCfunctional::is_spin_polarized ( ) const

inline

Returns true if the functional is spin_polarized.

References spin_polarized.

Referenced by plot().

static double XCfunctional::munge ( double rho )

inlinestaticprotected

References polyn().

Referenced by exc(), and vxc().

static void XCfunctional::munge2	(	double &	rho,
		double &	sigma
	)

inlinestaticprotected

References polyn().

static void XCfunctional::munge5	(	double &	rhoa,
		double &	rhob,
		double &	saa,
		double &	sab,
		double &	sbb
	)

inlinestaticprotected

References polyn().

static void XCfunctional::munge5_der	(	double &	rhoa,
		double &	rhob,
		double &	saa,
		double &	sab,
		double &	sbb,
		double &	drax,
		double &	dray,
		double &	draz,
		double &	drbx,
		double &	drby,
		double &	drbz
	)

inlinestaticprotected

References polyn().

static void XCfunctional::munge_der	(	double &	rhoa,
		double &	sigma,
		double &	drx,
		double &	dry,
		double &	drz
	)

inlinestaticprotected

References polyn().

void XCfunctional::plot ( ) const

inline

Crude function to plot the energy and potential functionals.

References exc(), madness::f, is_spin_polarized(), and vxc().

static void XCfunctional::polyn	(	const double	x,
		double &	p,
		double &	dpdx
	)

inlinestaticprotected

Smoothly switches between constant (x<xmin) and linear function (x>xmax)

$f(x,x_{\mathrm{min}},x_{\mathrm{max}}) = \left\{ \begin{array}{ll} x_{\mathrm{min}} & x < x_{\mathrm{min}} \\ p(x,x_{\mathrm{min}},x_{\mathrm{max}}) & x_{\mathrm{min}} \leq x_{\mathrm{max}} \\ x & x_{\mathrm{max}} < x \end{array} \right.$

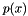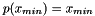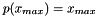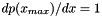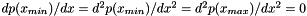where $p(x)$ is the unique quintic polynomial that satisfies $p(x_{min})=x_{min}$ , $p(x_{max})=x_{max}$ , $dp(x_{max})/dx=1$ , and $dp(x_{min})/dx=d^2p(x_{min})/dx^2=d^2p(x_{max})/dx^2=0$ .

References a(), b(), and c.

Referenced by munge(), munge2(), munge5(), munge5_der(), and munge_der().

madness::Tensor< double > XCfunctional::vxc	(	const std::vector< madness::Tensor< double > > &	t,
		const int	ispin,
		const int	what
	)		const

Computes components of the potential (derivative of the energy functional) at np points.

Any HF exchange contribution must be separately computed.

See the documenation of the exc() method for contents of the input t[] argument

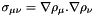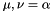We define $\sigma_{\mu \nu} = \nabla \rho_{\mu} . \nabla \rho_{\nu}$ with $\mu, \nu = \alpha$ or $\beta$ .

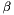For unpolarized GGA, matrix elements of the potential are 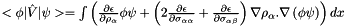$< \phi | \hat V | \psi > = \int \left( \frac{\partial \epsilon}{\partial \rho_{\alpha}} \phi \psi + \left( 2 \frac{\partial \epsilon}{\partial \sigma_{\alpha \alpha}} + \frac{\partial \epsilon}{\partial \sigma_{\alpha \beta}} \right) \nabla \rho_{\alpha} . \nabla \left( \phi \psi \right) \right) dx$

For polarized GGA, matrix elements of the potential are 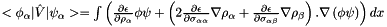$< \phi_{\alpha} | \hat V | \psi_{\alpha} > = \int \left( \frac{\partial \epsilon}{\partial \rho_{\alpha}} \phi \psi + \left( 2 \frac{\partial \epsilon}{\partial \sigma_{\alpha \alpha}} \nabla \rho_{\alpha} + \frac{\partial \epsilon}{\partial \sigma_{\alpha \beta}} \nabla \rho_{\beta} \right) . \nabla \left( \phi \psi \right) \right) dx$

Integrating the above by parts and assuming free-space or periodic boundary conditions we obtain that the local multiplicative form of the GGA potential is 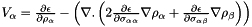$V_{\alpha} = \frac{\partial \epsilon}{\partial \rho_{\alpha}} - \left(\nabla . \left(2 \frac{\partial \epsilon}{\partial \sigma_{\alpha \alpha}} \nabla \rho_{\alpha} + \frac{\partial \epsilon}{\partial \sigma_{\alpha \beta}} \nabla \rho_{\beta} \right) \right)$

Until we get a madness::Function operation that can produce multiple results we need to compute components of the functional and potential separately:

Spin un-polarized
- what=0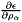 $\frac{\partial \epsilon}{\partial \rho_{\alpha}}$
- what=1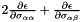 $2 \frac{\partial \epsilon}{\partial \sigma_{\alpha \alpha}} + \frac{\partial \epsilon}{\partial \sigma_{\alpha \beta}}$ (GGA only)
Spin polarized
- what=0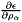 $\frac{\partial \epsilon}{\partial \rho_{\alpha}}$
- what=1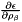 $\frac{\partial \epsilon}{\partial \rho_{\beta}}$
- what=2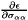 $\frac{\partial \epsilon}{\partial \sigma_{\alpha \alpha}}$
- what=3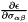 $\frac{\partial \epsilon}{\partial \sigma_{\alpha \beta}}$
- what=4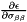 $\frac{\partial \epsilon}{\partial \sigma_{\beta \beta}}$

Parameters

[in]	t	The input densities and derivatives as required by the functional
[in]	what	Specifies which component of the potential is to be computed as described above