Spectral propagtor in time. Refer to documentation of file spectralprop.h for math detail. More...
#include <spectralprop.h>
Public Member Functions | |
| SpectralPropagator (int NPT) | |
Construct propagator using NPT points. More... | |
| ~SpectralPropagator () | |
| template<typename uT , typename expLT , typename NT > | |
| uT | step (double t, double Delta, const uT &u0, const expLT &expL, const NT &N, const double eps=1e-12, bool doprint=false, bool recurinit=true) |
Step forward in time from 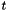 to to 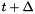 . More... . More... | |
Detailed Description
Spectral propagtor in time. Refer to documentation of file spectralprop.h for math detail.
Constructor & Destructor Documentation
|
inline |
Construct propagator using NPT points.
References madness::gauss_legendre().
|
inline |
Member Function Documentation
template<typename uT , typename expLT , typename NT >
|
inline |
Step forward in time from 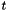 to
to 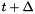 .
.
The template types should be automatically inferred from the invocation. uT is the C++ type for the solution.
- Parameters
-
[in] t The current time [in] Delta The time step [in] u0 The solution at the current time [in] expL A function or functor to compute 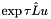 for
for 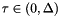
[in] N A function to compute the non-linear part [in] eps Threshold for convergence of iteration on norm of change in solution at last quadrature point. [in] doprint If true will print some info on convergence [in] recurinit If true initial guess is recursion from lower order quadrature instead of default explicit rule
- Returns
- The solution at time
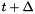
The user provided operators are invoked as
uT expL(double tau, const uT& u)
where 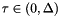 and
and
where 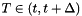 and
and  is a trial solution at time
is a trial solution at time 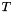 .
.
References k, N, and madness::print().
The documentation for this class was generated from the following file:
 1.8.8
1.8.8