embedded_dirichlet.cc File Reference

Provides test problems for examining the convergence of embedded (Dirichlet) boundary conditions. More...

#include <madness/mra/mra.h>
#include <madness/tensor/gmres.h>
#include <madness/muParser/muParser.h>
#include "test_problems.h"

Include dependency graph for embedded_dirichlet.cc:

Functions
int	main (int argc, char **argv)

Detailed Description

Provides test problems for examining the convergence of embedded (Dirichlet) boundary conditions.

Note

Full details of the mathematics of this routine can be found in M.G. Reuter et al., Comput. Phys. Commun. 183, pp. 1-7 (2012). This code can generate the data in Figures 1, 2, and 4 of that article.

The auxiliary PDE being solved is

where

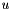• is the solution function
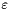• is the thickness of the boundary layer
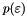• is the penalty prefactor, 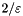seems to work well.
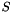• is the surface function
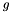• is the Dirichlet condition to be enforced on the surface
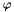• is the domain mask (1 inside, 0 outside, blurry on the border)
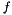• is the inhomogeneity.

The available test problems are

1. A sphere of radius 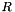with 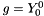, homogeneous (ConstantSphere)
2. A sphere of radius 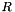with 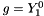, homogeneous (CosineSphere)
3. A sphere of radius 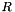with 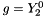, homogeneous (Y20Sphere)
4. A sphere of radius 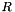with 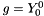, inhomogeneous 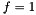(InhomoConstantSphere)

This program allows testing of various parameters,

1. The surface thickness
2. The penalty prefactor
3. The type of domain masking (LLRV or Gaussian)
4. The curvature / shape of the domain

for their effect on convergence of the solution.

Function Documentation

int main	(	int	argc,
		char **	argv
	)

References madness::LoadBalanceDeux< NDIM >::add_tree(), madness::Vector< T, N >::begin(), madness::WorldGopInterface::broadcast(), madness::Function< T, NDIM >::clear(), SafeMPI::COMM_WORLD, madness::copy(), mu::ParserBase::DefineVar(), DIRICHLET_RHS, DOMAIN_MASK, madness::error(), mu::ParserBase::Eval(), mpfr::fabs(), madness::finalize(), G, mu::ParserError::GetMsg(), madness::GMRES(), madness::World::gop, madness::initialize(), k, madness::LoadBalanceDeux< NDIM >::load_balance(), maxiter, madness::Function< T, NDIM >::norm2(), madness::World::rank(), madness::FunctionDefaults< NDIM >::redistribute(), madness::tr1::shptr::shared_ptr< T >::reset(), madness::FunctionDefaults< NDIM >::set_cubic_cell(), madness::FunctionDefaults< NDIM >::set_k(), madness::FunctionDefaults< NDIM >::set_thresh(), madness::FunctionDefaults< NDIM >::set_truncate_on_project(), mu::ParserBase::SetExpr(), madness::startup(), SURFACE, thresh, madness::Function< T, NDIM >::trace(), and uexact().