Collaboration diagram for Iterative solvers for linear/non-linear equations and optimizers:

Files
file	gmres.h
	Defines a general operator interface and a templated GMRES solver for solving linear equations.

file	solvers.h
	Defines interfaces for optimization and non-linear equation solvers.

Classes
struct	madness::SolverTargetInterface
	The interface to be provided by targets for non-linear equation solver. More...

struct	madness::OptimizationTargetInterface
	The interface to be provided by functions to be optimized. More...

struct	madness::SolverInterface
	The interface to be provided by solvers ... NOT USED ANYWHERE? More...

struct	madness::OptimizerInterface
	The interface to be provided by optimizers. More...

class	madness::SteepestDescent
	Unconstrained minimization via steepest descent. More...

class	madness::QuasiNewton
	Optimization via quasi-Newton (BFGS or SR1 update) More...

Functions
template<typename T >
Tensor< T >	madness::KAIN (const Tensor< T > &Q, double rcond=1e-12)
	Solves non-linear equation using KAIN (returns coefficients to compute next vector) More...

Detailed Description

Function Documentation

template<typename T >

Tensor<T> madness::KAIN	(	const Tensor< T > &	Q,
		double	rcond = `1e-12`
	)

Solves non-linear equation using KAIN (returns coefficients to compute next vector)

The Krylov-accelerated inexact-Newton method employs directional derivatives to estimate the Jacobian in the subspace and separately computes updates in the subspace and its complement.

We wish to solve the non-linear equations 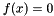$ f(x)=0 $ where $ f $ and $ x $ are vectors of the same dimension (e.g., consider both being MADNESS functions).

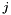Define the following matrices and vector (with $ i $ and $ j $ denoting previous iterations in the Krylov subspace and 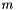$ m $ the current iteration):

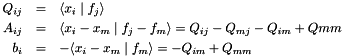
$\begin{eqnarray*} Q_{i j} & = & \langle x_i \mid f_j \rangle \\ A_{i j} & = & \langle x_i - x_m \mid f_j - f_m \rangle = Q_{i j} - Q_{m j} - Q_{i m} + Q{m m} \\ b_i & =& -\langle x_i - x_m \mid f_m \rangle = -Q_{i m} + Q_{m m} \end{eqnarray*}$

The subspace equation is of dimension 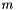$ m $ (assuming iterations are indexed from zero) and is given by

$A c = b$

The interior and exterior updates may be combined into one simple expression as follows. First, define an additional element of the solution vector

$c_m = 1 - \sum_{i<m} c_i$

and then the new vector (guess for next iteration) is given by

$x_{m+1} = \sum_{i \le m}{c_i ( x_i - f_i)}$

To employ the solver, each iteration

Compute the additional row and column of the matrix 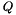that is the inner product between solution vectors ( 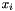) and residuals ( ).
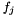Call this routine to compute the coefficients 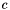and from these compute the next solution vector
Employ step restriction or line search as necessary to ensure stable/robust solution.

Parameters

[in]	Q	The matrix of inner products between subspace vectors and residuals.
[in]	rcond	Threshold for discarding small singular values in the subspace equations.

Returns: Vector for computing next solution vector

References b(), c, madness::gelss(), L, m, and std::tr1::T().

Referenced by madness::check_linear_dependence(), madness::NonlinearSolverND< NDIM >::update(), madness::XNonlinearSolver< T, C, Alloc >::update(), madness::SubspaceK< T, NDIM >::update_subspace(), madness::Subspace< T, NDIM >::update_subspace(), and madness::SCF::update_subspace().

Files

Classes

Functions

Detailed Description

Function Documentation